
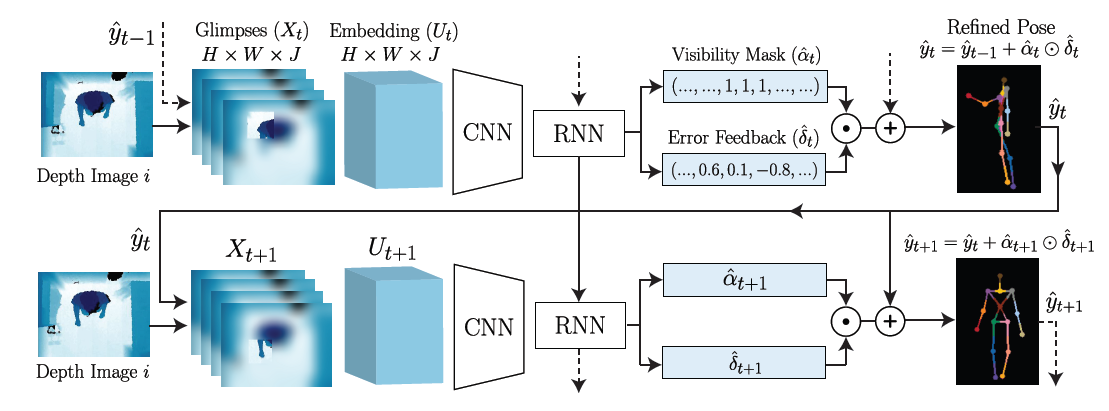
每个时间节点为一个阶段,每个阶段输入上一阶段的估测结果$\hat{y}_{t-1}$以及对原图处理产生的一个glimpse图像$X_t$。
- Local Input Representation
即将输入图片转化成glimpse图像。
Glimpse: $X\in \mathbb{R}^{H\times W\times J}$, 其中$H$和$W$表示glimpse图像的大小,$J$是关节点的数目。论文里将glimpse图像比喻成视网膜,它是一种中心较清晰,边缘较模糊的图像编码方式。这让中心的特征可以被focus,同时能够保留部分空间信息。
第一步:从输入的深度图像中围绕每个预测的身体部位抽取一系列patch。第二步:将这些patch转化为glimpse。
- Learned Viewpoint Invariant Embedding
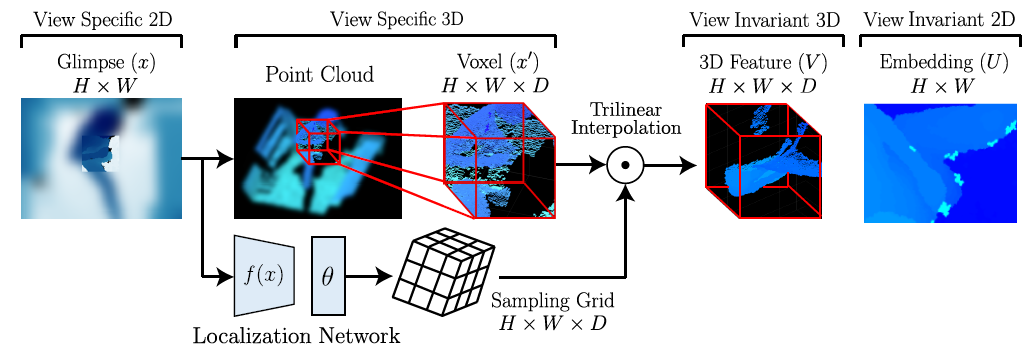
将glimpse图像投射到一个预训练的固定视角的特征空间。
首先把每一个glimpse图像$x\in H\times W$转化为三维像素(体素)$x’\in H\times W\times D$,其中$D$是体素的深度。体素只表示深度图,并不能表示一个完整的3D模型。我们还要将其映射到固定视角的特征空间来产生最终的3D模型。
这个映射的过程就是空间变换网络(Spatial Transformer Networks)的过程。分为两步。第一步:用一个定位网络(localization network)$f(\cdot)$来估测一个3D变换的参数$\theta$。第二步:计算一个采样网格(sampling grid) $G\in \mathbb{R}^{H\times W\times D}$。最终得到feature map:
$$V_{ijk}=\sum_{a=1}^{H}\sum_{b=1}^{W}\sum_{c=1}^{D}x’_{abc}\mathrm{ker}\left(\frac{a-x_{ijk}^{(G)}}{H}\right)\mathrm{ker}\left(\frac{b-y_{ijk}^{(G)}}{W}\right)\mathrm{ker}\left(\frac{c-z_{ijk}^{(G)}}{D}\right)$$
其中$\mathrm{ker}(\cdot)=\mathrm{max}(0,1-|\cdot|)$,表示三线性采样核。最后将固定视角的3D feature map $V \in \mathbb{R}^{H \times W \times D}$ 映射到固定视角的2D feature map $U\in \mathbb{R}^{H \times W}$:
$$U_{ij}=\sum_{c=1}^DV_{ijc}$$
$V$是对glimpse的3D特征表达,$U$是$V$映射回二维空间的embedding结果。
- Convolutional and Recurrent Networks
所有得到的$U$组成了一个$H\times W\times J$的向量。但是直接回归人体部位的位置由于高度非线性映射的问题很难实现,所以采用了一个逐步修正估测结果的方法。为了让时序信息表示更加直接,关联性更强,用LSTM模型连接相邻两步。
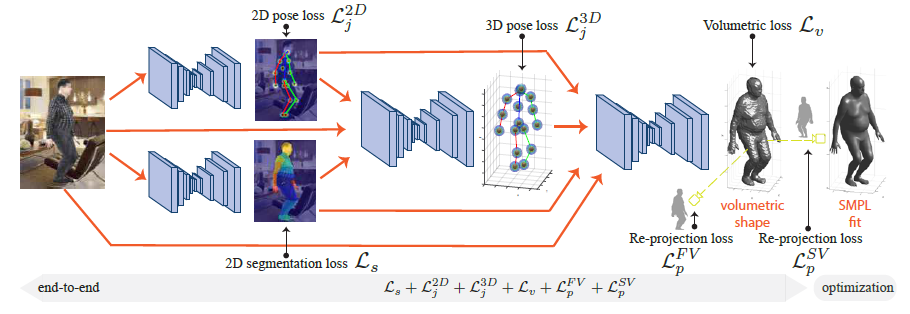
包含独立训练的四个子网络,分别用来生成2D姿态、2D分割, 3D姿态, 3D形状。
这篇论文使用了四种loss function:3D体积测量loss$\mathcal{L}_v$ 、再投影loss$\mathcal{L}_p$、 姿态loss$\mathcal{L}_j$、分割loss$\mathcal{L}_s$。
- Volumetric Inference for 3D Human Shape
使用“体素表示法”,估测3D形状的子网络输出一个体素网格上的占用图,代表每个网格是否被填满。首先要调整图片的位置和大小,使网格的中心也就是$z$轴的位置大致在人体的髋关节附近,大小根据2D分割的结果来调整。
$V$表示要训练的网络占用图经过sigmoid激活后的值,$\hat{V}$是它的ground truth,$\mathcal{L}_v$定义为二者之间的交叉熵:
$$\mathcal{L}_v=\sum_{x=1}^W\sum_{y=1}^H\sum_{z=1}^DV_{xyz}\mathrm{log}\hat{V}_{xyz}+(1-V_{xyz})\mathrm{log}(1-\hat{V}_{xyz})$$
占用图是二分类问题,可以推广至多分类问题,比如七分类(头、躯干、左腿、右腿、左臂、右臂、背景)就可以做人体3D分割。
- Multi-view Re-projection Loss On the Silhouette
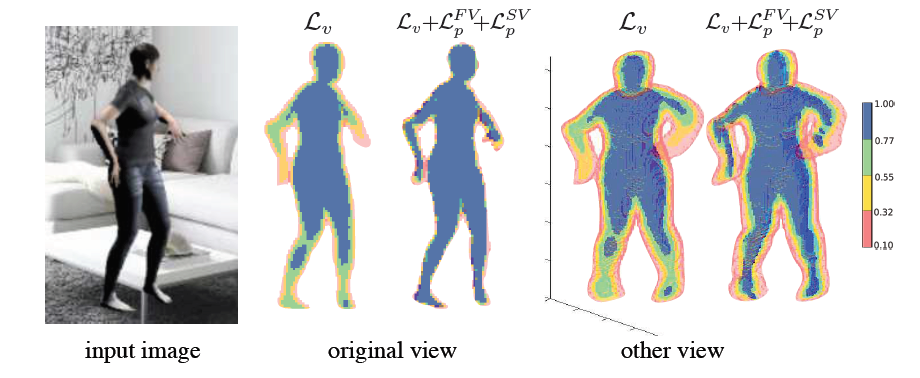
四肢的confidence较低,因此采用2D再投影loss,增加边界体素的重要性。定义正投射(Front View Projection)和侧投射(Side View Projection),即分别取$z$轴和$x$轴的最大值:
$$\hat{S}^{FV}(x,y)=\max\limits_{z}\hat{V}_{xyz}$$
$$\hat{S}^{SV}(y,z)=\max\limits_{x}\hat{V}_{xyz}$$
$S^{FV}$和$S^{SV}$同理。$\mathcal{L}_p$依然定义为交叉熵:
$$\mathcal{L}_p^{FV}=\sum_{x=1}^W\sum_{y=1}^HS(x,y)\mathrm{log}\hat{S}^{FV}(x,y)+(1-S(x,y))\mathrm{log}(1-\hat{S}^{FV}(x,y))$$
$$\mathcal{L}_p^{SV}=\sum_{y=1}^H\sum_{z=1}^DS(y,z)\mathrm{log}\hat{S}^{SV}(y,z)+(1-S(y,z))\mathrm{log}(1-\hat{S}^{SV}(y,z))$$
- Multi-task Learning with Intermediate Supervision
2D姿态loss:用沙漏网络的前两层将$3\times256\times256$的RGB图像映射到$16\times64\times64$的2D关节热度图,其中$16$为关节数。这$16$张热度图是以每个关节为中心的高斯分布,放在一起取最大值就得到最终的2D关节定位热度图。$\mathcal{L}_{j}^{2D}$定义为关节定位热度图和ground truth之间的均方差。
2D分割loss:依然是用沙漏网络的前两层,将$3\times256\times256$的RGB图像映射到$15\times64\times64$的热度图,其中$15$为人体部位数。训练集基于一个叫做Skinned Multi-person Linear Model (SMPL)的模型。$\mathcal{L}_{s}$定义为人体部位定位热度图和ground truth之间的交叉熵。
3D姿态loss:将2D热度图延伸到3D,在体素网格上用3D的高斯分布表示3D关节定位。其中$xy$平面上就是2D的关节热度图,$z$轴上的值代表深度。实验表明,深度范围是一个大约85cm的区间,最多占用$19$位。所以最终的3D关节定位热度图大小为$64\times64\times19$。同样$\mathcal{L}_{j}^{3D}$定义为关节定位热度图和ground truth之间的均方差。
最后总的loss为:
$$\mathcal{L}=\lambda_{j}^{2D}\mathcal{L}_{j}^{2D}+\lambda_{s}\mathcal{L}_{s}+\lambda_{j}^{3D}\mathcal{L}_{j}^{3D}+\lambda_{v}\mathcal{L}_{v}+\lambda_{p}^{FV}\mathcal{L}_{p}^{FV}+\lambda_{p}^{SV}\mathcal{L}_{p}^{SV}$$
规定这些系数的比例$(\lambda_{j}^{2D},\lambda_{s},\lambda_{j}^{3D},\lambda_{v},\lambda_{p}^{FV},\lambda_{p}^{SV})\propto (10^7,10^3,10^6,10^1,1,1)$,让每个loss的平均梯度在微调开始时处于同一尺度。同时参数的和保持为$1$。